昨天看到这样一句话

“密码本质上就是拉开了时间复杂度的差距。”

初次看到，茫然不知，我想，密码跟时间复杂度究竟有何联系？何为复杂度？这复杂程度的参照物又是什么？怀揣着疑问，我在知乎、CSDN上阅读几篇大佬对密码学的认识与理解。阅读归阅读，还是得靠吸收与总结，那现在就开始我对密码学cryptography中RSA的深入浅出吧！（密码学的背景发展史等，网上千篇一律，暂不赘述

时间复杂度

先说说开头提到的这句哈把“密码本质上就是拉开了时间复杂度的差距。”我们知道，计算机的计算运行速度很快，四位数乘四位数的计算，人需要一分钟左右，而计算机秒出结果。然而，计算机的计算能力是有限的，就算是超级计算机“天问二号”，计算速度也有上限

所以对于计算机来说，我们需要利用时间复杂度来衡量一个程序的算法有多耗时。按照初中学过的知识，我们知道底数大于1的指数呈“爆炸式增长”，也从古代国王在64个格子放米的例子中可以看出，当放到第28格的时候，需要米已经超过1亿，放到第64格的时候，大约要放92亿粒！（有人计算过，大约是2814亿吨重）从这个例子我们就可以看到，时间复杂度直接影响了程序完成的速度。当计算机计算指数函数10的n次方时，可能就需要好几十年

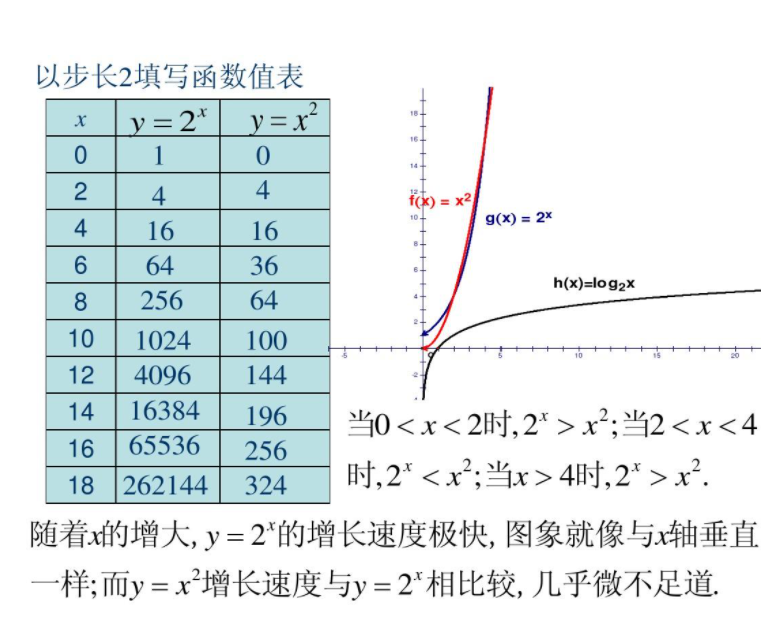
从而可知，在密码学中，很多时候密码不是不可以破解的，只不过破解密码需要大量的时间。

比如在RSA中最关键的一步，是Alice生成两个指数p和q，计算它们乘积n=p*q，然后告诉Bob这个n的值，他就需要把n质因数分解为p和q，对于这种单项函数来说，逆着运算（即分解质因数)的时间复杂度是指数级，比顺着运算（乘积n）的运算时间来得要长。

假如Alice的这个p和q足够大，等Bob分解完n，恐怕就过去了好几十年。

因此，密码的本质上就是拉开了时间复杂度的差距，使得解密密码的时间复杂度高于加密的时间复杂度，以达成保密的目的。

一些数论

来，先来膜拜一下伟大的数学家—欧拉

欧拉

被称为“对世界数学的发展作出创造性工作的人士”，他值得！

下述的一些数论知识在初高中就有学习过，简单提一哈~

欧拉函数—φ（n）

φ（n）：在[0,n)中与n互质的正整数的个数

eg：n=23，在[0,23)中，与21互质的正整数有：1、 2、 4 、5 、8、 10、 11 、13、 16 、17、 19、 20这12个数，因此φ（23）=12

φ（n）=（p-1）（q-1）

eg：23=7*3，φ（23）=（7-1）（3-1）=12

同余式

我们学过余数，同余式就是另外一种写法罢了，下面以一个表格做出比较

名称 余式 同余式
eg1 23÷7=3…2 23≡2（mod7）
eg2 50÷8=6…2 50≡2（mod8）
通式 a÷m=k…b a≡b（mod m）

之前学习同余式可能忽略了几个性质，网上找了一下基本性质，直接放图

Snipaste_2021-07-23_10-28-39

欧拉公式

若a与n互质，则a^φ（n）^≡1（mod n）

乘法逆元

如果ab ≡ 1（mod m），则称a和b为关于m互为乘法逆元

已知a求b的方法：因为ab ≡ 1（mod m），所以不妨设ab+mk=1，其中a和m为已知数。可以利用扩展欧几里得算法，计算出来一个乘法逆元b。

RSA简介

前面铺垫了这么这么多，终于开始进入咱们的正题—RSA的深入浅出

先对rsa密钥体制做个介绍

1、选择两个大的互质参数p，q，计算出模数n=p*q

2、计算欧拉函数φ（n）=（p-1)(q-1)。选择一个e（1<e<φ（n)),要求e和φ（n）互质，即gcd(e,φ（n）)=1

3、计算e的模反数d。计算方法为e*d≡1（mod φ（n））【模反元素：如果存在两个正整数e和φ（n）互质，那么一定存在一个整数d，使得ed-1被φ（n）整除，即ed=kφ（n）+1.这是，d就是e的模反元素。欧拉公式可以证明模反元素必然存在。两个整数a，b，它们除以整数φ（n）所得余数相等，即a≡1(modφ（n）)，b≡1（modφ（n）），根据相乘的性质ab≡1（modφ（n）），所以a和b互为逆元

4、对明文m加密。密文c=pow（m，e，n），等同于c=m^e^（mod n）

5、对密文c解密。明文m=pow（c，d，n），等同于m=c^d^（mod n）

RSA安全性分析

值得一提的是，虽然公钥（n，e）是直接公开的，但是只有Alice知道密钥（n，d），可以计算m=c^d^（mod n），除了Alice，没有任何人可以知道φ(n)，所以没有人可以求出e关于φ(n)的乘法逆元d。也就是说d的值从头到尾只有Alice自己知道，不可能泄露。假如Alice把本地的私钥弄丢了，那，谁也解不开密码，这就是非对称密码rsa与对称密码的本质区别

常用的攻击方法

直接分解模数

基本原理

直接分解数模n是最直接的攻击放方法，也是最困难的办法。破解RSA最直接（暴力）的方法就是分解整数n，然后计算欧拉函数φ(n)=(p-1) (q-1),再通过d e ≡ 1 mod φ(N)，即可计算出 d，然后就可以使用私钥(N, d)通过m = pow(c,d,N)解密明文。

如果n小于256bit，可以使用本地工具进行暴力分解，例如windwods平台的RSATool，可以在数分钟之内完成256bit的n的分解。
如果n大于768bit，可以尝试利用在线网站http://factordb.com， 这一类在线网站的原理是储存了部分n分解成功的的值。

CTF原题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
{920139713,19}

704796792
752211152
274704164
18414022
368270835
483295235
263072905
459788476
483295235
459788476
663551792
475206804
459788476
428313374
475206804
459788476
425392137
704796792
458265677
341524652
483295235
534149509
425392137
428313374
425392137
341524652
458265677
263072905
483295235
828509797
341524652
425392137
475206804
428313374
483295235
475206804
459788476
306220148

分解n可以通过在线网站http://www.factordb.com/index.php。

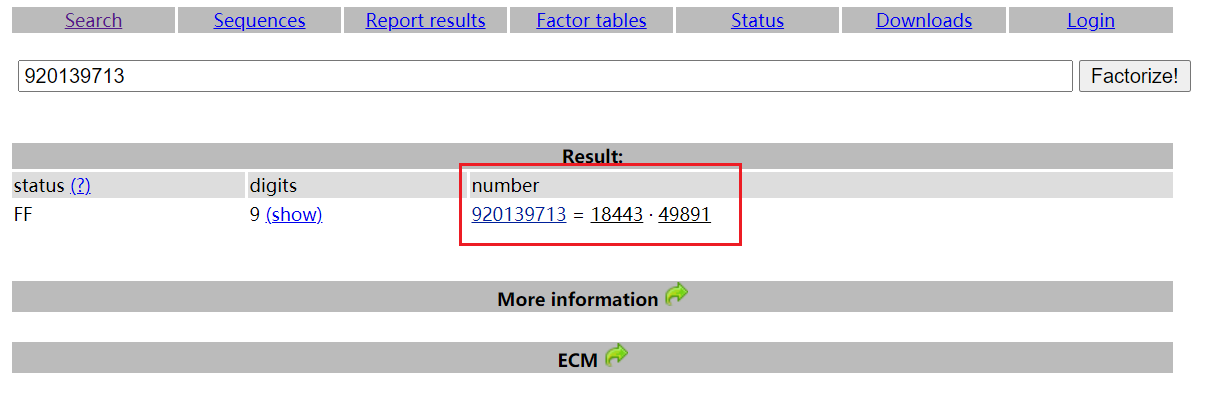
Snipaste_2021-07-23_11-42-13

p=18443,q=49891,e=19,c=这一大串数字密文

因此可以通过d * e ≡ 1 mod φ(n)，计算出 d

1
2
3
4
5
6
7
8
import gmpy2
p = gmpy2.mpz(18443)     #初始化大整数
q = gmpy2.mpz(49891)
e = gmpy2.mpz(19)
phi_n = (p-1)*(q-1)
d = gmpy2.invert(e,phi_n)    #invert（e， φ(n)）返回d使得e*d == 1 mod φ(n)，如果不存在d，则返回0
print("p=%s,q=%s,e=%s"%(p,q,e))
print("d is:\n%s"%d)
1
2
3
4
#输出结果为
p=18443,q=49891,e=19 
d is: 
96849619

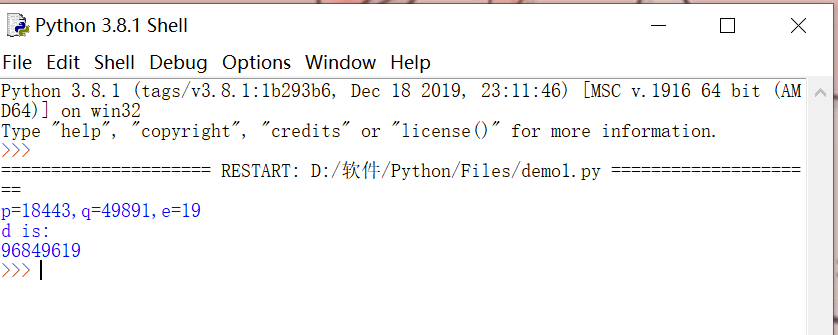
到目前为止，有了d就可以求出明文m

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#求明文
import gmpy2
n = 920139713
d = 96849619
c = """
704796792
752211152
274704164
18414022
368270835
483295235
263072905
459788476
483295235
459788476
663551792
475206804
459788476
428313374
475206804
459788476
425392137
704796792
458265677
341524652
483295235
534149509
425392137
428313374
425392137
341524652
458265677
263072905
483295235
828509797
341524652
425392137
475206804
428313374
483295235
475206804
459788476
306220148
"""
result = ""
c_list = c.split()
#print(c_list)
for i in c_list:
    result += chr(pow(int(i),d,n))
print(result)

解密结果

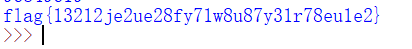
对rsa的公共模数攻击

使用相同的模数n，取不同的e1、e2，用不同的私钥d1、d2加密同一份明文消息，得到不同的密文c1、c2

基本原理

假如采用两个或者两个以上的公钥(n，e)来加密同一条信息，可以得到下面的结论：

c1 = pow(m, e1, n)
c2 = pow(m, e2, n)

分别拿对应的私钥来加密，可以得到相同的明文m

m = pow(c1, d1, n)
m = pow(c2, d2, n)

假设攻击者已知n,e1,e2,c1,c2，即可以得到明文m，因为e1和e2互质，所以使用欧几里得算法（用于计算两个整数a,b的最大公约数）可以找到能够满足以下条件的x，y：

pow(x,e1)+pow(y,e2)=1

假设x为负数，需再使用欧几里得算法来计算

pow(c1,-1)

则可以得到

pow(pow(c1,-1),-x) * pow(c2,y) = p mod(n)

如果p<n，则p可以被计算出来。

rsa小指数e攻击

如果RSA系统的公钥e选取较小的值，比如e=3，就容易受到攻击。

有三个分别使用不同的模数n1,n2,n3，但是都选取e=3，加密同一个明文可以得到：

c1 = pow(m,3,n1)
c2 = pow(m,3,n2)
c3 = pow(m,3,n3)

一般情况下，n1,n2,n3互素，否则会比较容易求出公因子，从而安全性大幅度的减低。

ras选择密文攻击

在此种攻击模型中，攻击者需要掌握的内容包括：加密算法、截获的部分密文、自己选择的密文消息以及相应的被解密的明文。

利用公约数

思路

如果两次加密的n1和n2具有相同的素因子，可以利用欧几里德算法直接分解n1和n2，通过欧几里德算法计算出两个n的最大公约数p

1
2
3
4
5
6
7
8
9
10
11
12
def gcd(a, b):
	if a < b:
    	a, b = b, a
	while b != 0:
    	temp = a % b
     	a = b
     	b = temp
def gcd_digui(a, b):
	if b != 0:
   		return a
	return gcd(b,a%b)
p = gcd(n1,n2)

识别

识别此类题目，通常会发现题目给了若干个n，均不相同，并且都是2048bit，4096bit级别，无法正面硬杠，并且明文都没什么联系，e也一般取65537。

例题

n1=9051013965404084482870087864821455535159008696042953021965631089095795348830954383127323853272528967729311045179605407693592665683311660581204886571146327720288455874927281128121117323579691204792399913106627543274457036172455814805715668293705603675386878220947722186914112990452722174363713630297685159669328951520891938403452797650685849523658191947411429068829734053745180460758604283051344339641429819373112365211739216160420494167071996438506850526168389386850499796102003625404245645796271690310748804327
n2=13225948396179603816062046418717214792668512413625091569997524364243995991961018894150059207824093837420451375240550310050209398964506318518991620142575926623780411532257230701985821629425722030608722035570690474171259238153947095310303522831971664666067542649034461621725656234869005501293423975184701929729170077280251436216167293058560030089006140224375425679571181787206982712477261432579537981278055755344573767076951793312062480275004564657590263719816033564139497109942073701755011873153205366238585665743

我们用欧几里得算法计算出n1n2的最大公约数p:

代码

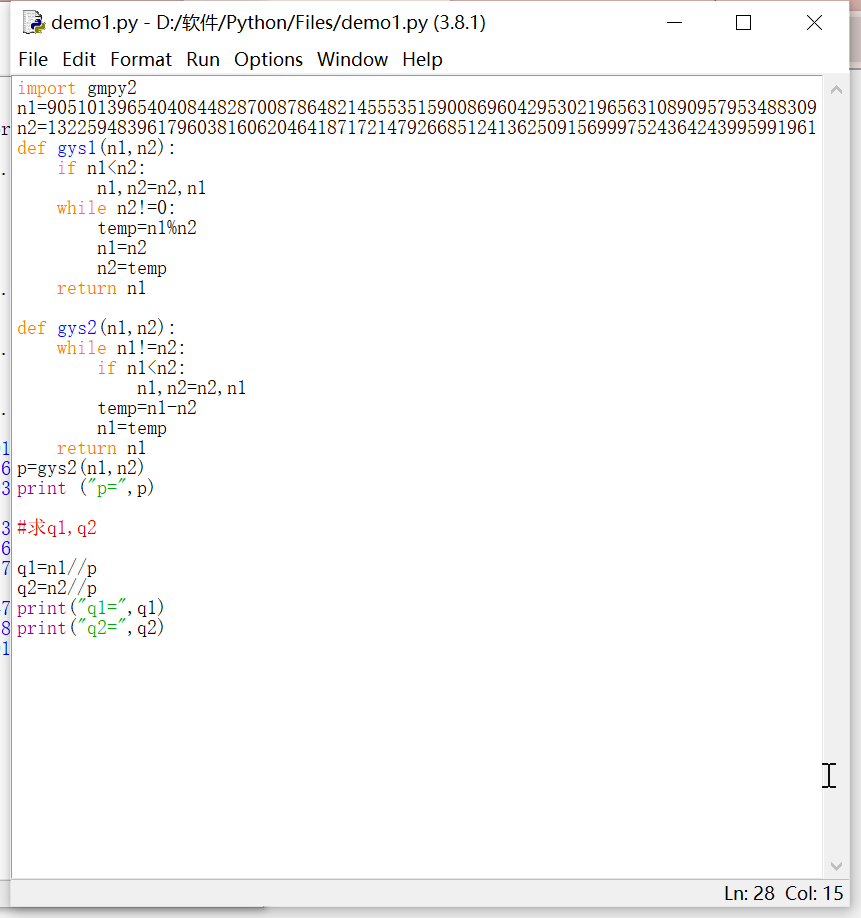
p=1564859779720039565508870182569324208117555667917997801104862601098933699462849007879184203051278194180664616470669559575370868384820368930104560074538872199213236203822337186927275879139590248731148622362880471439310489228147093224418374555428793546002109

在求出

计算结果

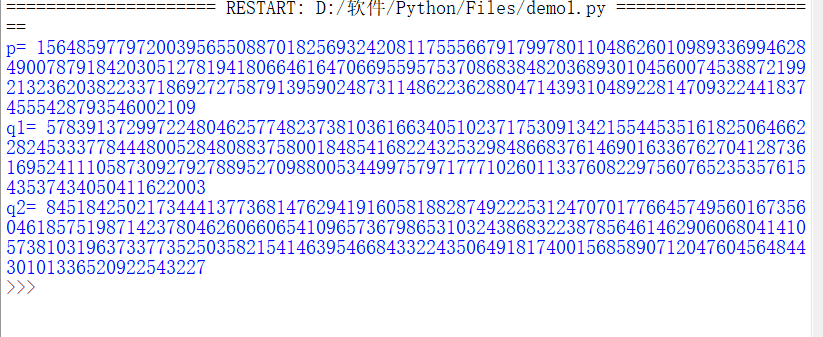
q1=5783913729972247946253435353096326443704028481940849421114868598345923360618656121534285508526073359609714402851036717793499213802965059543550823534771936528992718924827788759885479930993068821959532735506613731118802093419664455101954524961474681210142720

q2=8451842502173444137736814762941916058188287492225312470701776645749560167356046185751987142378046260660654109657367986531032438683223878564614629060680414105738103196373377352503582154146395466843322435064918174001568589071204760456484430101336520922543227

有了p、q、n、e，再用常规的方法求出d

d is:
765380157716548443425596742911266886410191216178112356262846713847378783683172254263632491551899451289816619131919308216828436088806741843938280790265785398475478529787399443730855951368875915938248660455496573500895189591415557910142785245074081094025796970799530756594690014890734289131423703767389303315127407756913225666969130239449802975261679436688682166951981930860230211054980705709388431034038355036001994657320535672433358165972446575669374989675751263007447610176671622049636459417182325418702702105

感叹一下，数字真的好大！

Coppersmith定理攻击

在一个e阶的mod n多项式f(x)中，如果有一个根小于n^frac{1}{e} ，就可以运用一个O(log n)的算法求出这些根。

这个定理可以应用于RSA算法。如果e = 3并且在明文当中只有三分之二的bite是已知的，这种算法可以求出明文中所有的bite

工具之在线分解大素数：http://factordb.com

CTF-RSA-tool: https://github.com/D001UM3/CTF-RSA-tool

参考文章：https://blog.csdn.net/huanghelouzi/article/details/82943615

安装gmpy2：https://blog.51cto.com/u_12332766/2116615

sagemath:http://www.sagemath.org/ (我还没装，暂时没用上)