hash，一般翻译做“散列”，也有直接音译为”哈希”

就是把任意长度的输入通过散列算法，变换成固定长度的输出，该输出就是散列值。

MD（Message Digest )，为计算机安全领域广泛使用的一种散列函数，用以提供消息的完整性保护。目前广泛使用的是第五版，因此也被称为MD5。

MD5和SHA1可以说是目前应用最广泛的Hash算法，而它们都是以MD4为基础设计的。

MD5的典型应用是对一段Message(字节串)产生fingerprint(指纹），以防止被“篡改”。

举个例子，你将一段话写在一个叫 readme.txt文件中，并对这个readme.txt产生一个MD5的值并记录在案，然后你可以传播这个文件给别人，别人如果修改了文件中的任何内容，你对这个文件重新计算MD5时就会发现（两个MD5值不相同）。如果再有一个第三方的认证机构，用MD5还可以防止文件作者的“抵赖”，这就是所谓的数字签名应用。

MD5加解密

在线网站MD5在线加密/解密/破解—MD5在线 (sojson.com)

明文是2021加密后

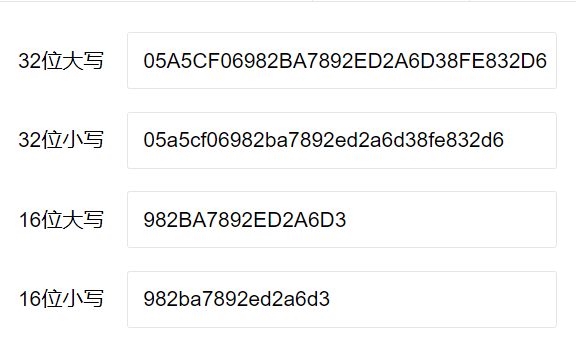
选取任意一组密文进行解密

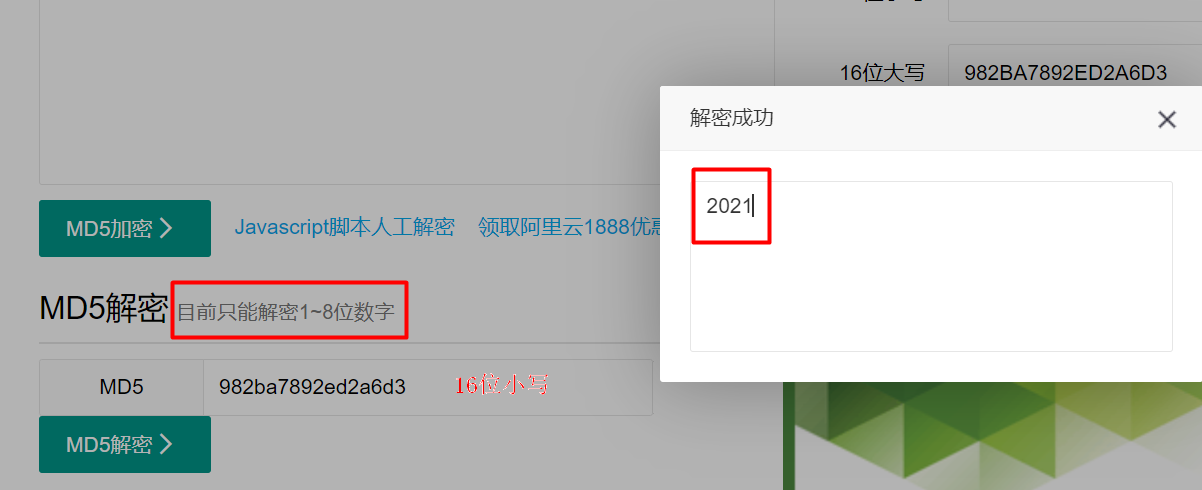
但是稍微复杂一点的字母就解不出来了唉

Hash算法MD5分析

MD5算法的原理

对MD5算法简要的叙述可以为：MD5以512位分组来处理输入的信息，且每一分组又被划分为16个32位子分组，经过了一系列的处理后，算法的输出由四个32位分组组成，将这四个32位分组级联后将生成一个128位散列值。

首先是对信息进行填充，使其位长对512求余的结果=448

因此，原来信息的位长应该为N*512+448

填充的方法：在原信息后补一个1和许多0，直到满足条件

填充完毕后，在这个结果后面加一个以64位二进制表示的填充前的信息长度

因此，现在的消息位长=N512+448+64=(N+1)512，这样的长度刚好是512的整数倍

流程图如下：

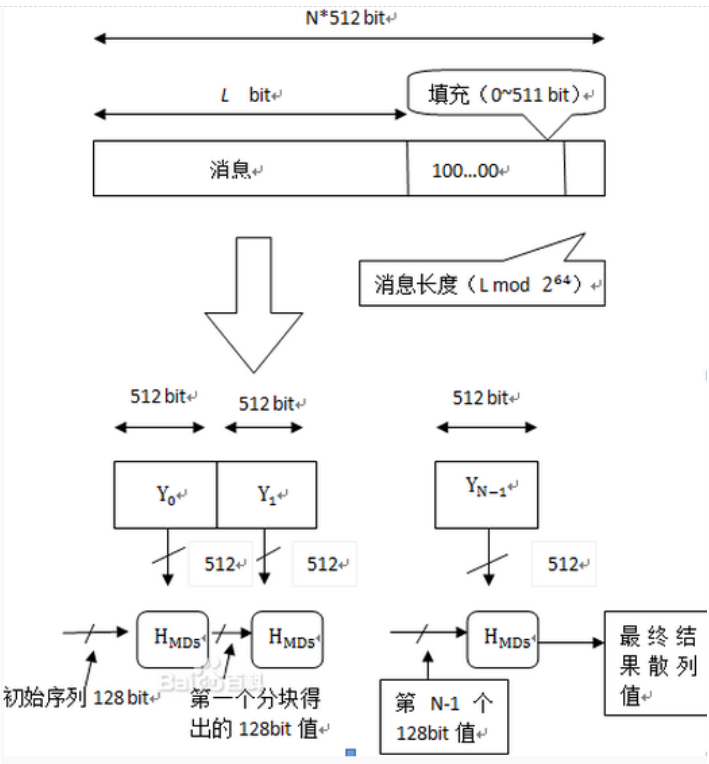
表示第i个分组，每次的运算都由前一轮的128位结果值和第i块512bit值进行运算。初始的128位值为初始链接变量，这些参数用于第一轮的运算，他们分别为：A=0x01234567，B=0x89ABCDEF，C=0xFEDCBA98，D=0x76543210。

每一分组的算法流程如下：

第一分组需要将上面四个链接变量复制到另外四个变量中：

A到a，B到b，C到c，D到d。

从第二分组开始的变量为上一分组的运算结果。

主循环有四轮（MD4只有三轮），每轮循环都很相似。第一轮进行16次操作。每次操作对a、b、c和d中的其中三个作一次非线性函数运算，然后将所得结果加上第四个变量，文本的一个子分组和一个常数。再将所得结果向左环移一个不定的数，并加上a、b、c或d中之一。最后用该结果取代a、b、c或d中之一。

以一下是每次操作中用到的四个非线性函数（每轮一个）。

F(X,Y,Z) =(X&Y)|((~X)&Z)
G(X,Y,Z) =(X&Z)|(Y&(~Z))
H(X,Y,Z) =X^Y^Z
I(X,Y,Z)=Y^(X|(~Z))
#（&；是与，|是或，~是非，^是异或）

这四个函数的说明：如果X、Y和Z的对应位是独立和均匀的，那么结果的每一位也应是独立和均匀的。

F是一个逐位运算的函数。即，如果X，那么Y，否则Z。函数H是逐位奇偶操作符。

假设Mj表示消息的第j个子分组（从0到15），常数ti是4294967296*abs(sin(i)）的整数部分，i取值从1到64，单位是弧度。（4294967296等于2的32次方）

FF(a,b,c,d,Mj,s,ti）表示 a = b + ((a + F(b,c,d) + Mj + ti) << s)

GG(a,b,c,d,Mj,s,ti）表示 a = b + ((a + G(b,c,d) + Mj + ti) << s)

HH(a,b,c,d,Mj,s,ti）表示 a = b + ((a + H(b,c,d) + Mj + ti) << s)

Ⅱ（a,b,c,d,Mj,s,ti）表示 a = b + ((a + I(b,c,d) + Mj + ti) << s)

这四轮（64步）是：

第一轮

FF(a,b,c,d,M0,7,0xd76aa478）
FF(d,a,b,c,M1,12,0xe8c7b756）
FF(c,d,a,b,M2,17,0x242070db)
FF(b,c,d,a,M3,22,0xc1bdceee)
FF(a,b,c,d,M4,7,0xf57c0faf)
FF(d,a,b,c,M5,12,0x4787c62a)
FF(c,d,a,b,M6,17,0xa8304613）
FF(b,c,d,a,M7,22,0xfd469501）
FF(a,b,c,d,M8,7,0x698098d8）
FF(d,a,b,c,M9,12,0x8b44f7af)
FF(c,d,a,b,M10,17,0xffff5bb1）
FF(b,c,d,a,M11,22,0x895cd7be)
FF(a,b,c,d,M12,7,0x6b901122）
FF(d,a,b,c,M13,12,0xfd987193）
FF(c,d,a,b,M14,17,0xa679438e)
FF(b,c,d,a,M15,22,0x49b40821）

第二轮

GG(a,b,c,d,M1,5,0xf61e2562）
GG(d,a,b,c,M6,9,0xc040b340）
GG(c,d,a,b,M11,14,0x265e5a51）
GG(b,c,d,a,M0,20,0xe9b6c7aa)
GG(a,b,c,d,M5,5,0xd62f105d)
GG(d,a,b,c,M10,9,0x02441453）
GG(c,d,a,b,M15,14,0xd8a1e681）
GG(b,c,d,a,M4,20,0xe7d3fbc8）
GG(a,b,c,d,M9,5,0x21e1cde6）
GG(d,a,b,c,M14,9,0xc33707d6）
GG(c,d,a,b,M3,14,0xf4d50d87）
GG(b,c,d,a,M8,20,0x455a14ed)
GG(a,b,c,d,M13,5,0xa9e3e905）
GG(d,a,b,c,M2,9,0xfcefa3f8）
GG(c,d,a,b,M7,14,0x676f02d9）
GG(b,c,d,a,M12,20,0x8d2a4c8a)

第三轮

HH(a,b,c,d,M5,4,0xfffa3942）
HH(d,a,b,c,M8,11,0x8771f681）
HH(c,d,a,b,M11,16,0x6d9d6122）
HH(b,c,d,a,M14,23,0xfde5380c)
HH(a,b,c,d,M1,4,0xa4beea44）
HH(d,a,b,c,M4,11,0x4bdecfa9）
HH(c,d,a,b,M7,16,0xf6bb4b60）
HH(b,c,d,a,M10,23,0xbebfbc70）
HH(a,b,c,d,M13,4,0x289b7ec6）
HH(d,a,b,c,M0,11,0xeaa127fa)
HH(c,d,a,b,M3,16,0xd4ef3085）
HH(b,c,d,a,M6,23,0x04881d05）
HH(a,b,c,d,M9,4,0xd9d4d039）
HH(d,a,b,c,M12,11,0xe6db99e5）
HH(c,d,a,b,M15,16,0x1fa27cf8）
HH(b,c,d,a,M2,23,0xc4ac5665）

第四轮

Ⅱ（a,b,c,d,M0,6,0xf4292244）
Ⅱ（d,a,b,c,M7,10,0x432aff97）
Ⅱ（c,d,a,b,M14,15,0xab9423a7）
Ⅱ（b,c,d,a,M5,21,0xfc93a039）
Ⅱ（a,b,c,d,M12,6,0x655b59c3）
Ⅱ（d,a,b,c,M3,10,0x8f0ccc92）
Ⅱ（c,d,a,b,M10,15,0xffeff47d)
Ⅱ（b,c,d,a,M1,21,0x85845dd1）
Ⅱ（a,b,c,d,M8,6,0x6fa87e4f)
Ⅱ（d,a,b,c,M15,10,0xfe2ce6e0)
Ⅱ（c,d,a,b,M6,15,0xa3014314）
Ⅱ（b,c,d,a,M13,21,0x4e0811a1）
Ⅱ（a,b,c,d,M4,6,0xf7537e82）
Ⅱ（d,a,b,c,M11,10,0xbd3af235）
Ⅱ（c,d,a,b,M2,15,0x2ad7d2bb)
Ⅱ（b,c,d,a,M9,21,0xeb86d391）

所有这些完成之后，将A、B、C、D分别加上a、b、c、d。然后用下一分组数据继续运行算法，最后的输出是A、B、C和D的级联。

当你按照我上面所说的方法实现MD5算法以后，你可以用以下几个信息对你做出来的程序作一个简单的测试，看看程序有没有错误。

MD5 ("") = d41d8cd98f00b204e9800998ecf8427e
MD5 ("a") = 0cc175b9c0f1b6a831c399e269772661
MD5 ("abc") = 900150983cd24fb0d6963f7d28e17f72
MD5 ("message digest") =f96b697d7cb7938d525a2f31aaf161d0
MD5 ("abcdefghijklmnopqrstuvwxyz") 
= c3fcd3d76192e4007dfb496cca67e13b
MD5 ("ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz")
=f29939a25efabaef3b87e2cbfe641315