运算方法和运算部件
主要内容
第3章(运算方法和运算部件〉主要介绍各类定点数和浮点数的运算方法和相应的运算部件 ,以及核心运算部件ALU的功能和设计实现等。
头一回计组课上就能听懂,之前都是课后花时间补救的>_<
因此 今天是复习而不是预习!必须趁热打铁写个笔记
核心运算部件ALU
基本运算部件:加法器、ALU、移位器,ALU的核心部件是加法器
要看懂书上的图解前,得先知道一些集成电路的逻辑符号和数学运算符(破案了!上一节上课听不懂的原因
常用集成电路逻辑符号对照表
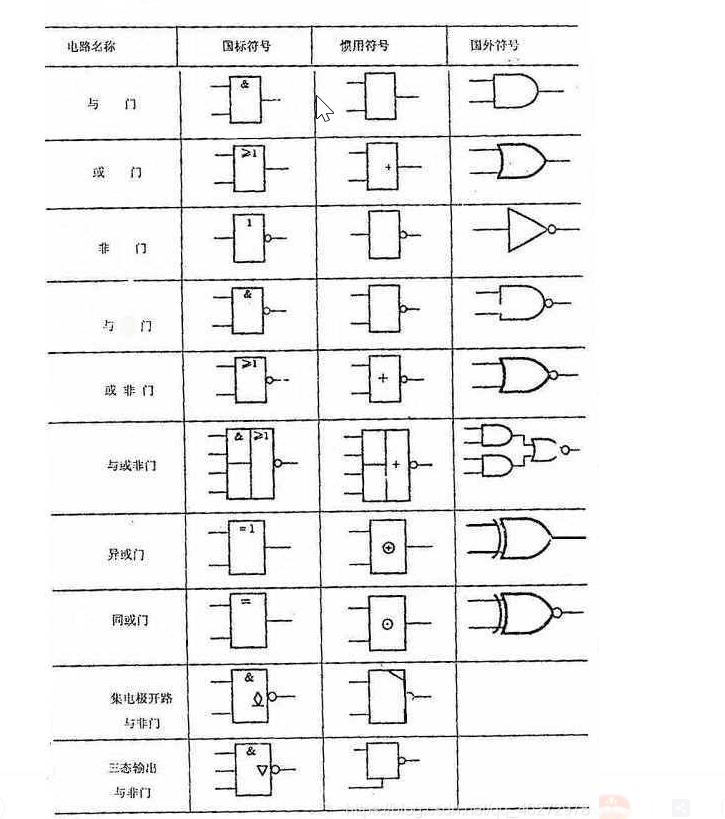
基本数学运算
异或(xor),数学符号为“⊕”,相同为假,不同为真。
1 | 若x=0101B,y=1011B |
同或,数学符号为⊙,相同为真,不同为假
1 | 若x=0101B,y=1011B |
与非,与+非,都为1时输出0
或非,或+非,都为1时输出1
串行进位加法器
1 | #Fi:全加和 Ci:全加进位 |
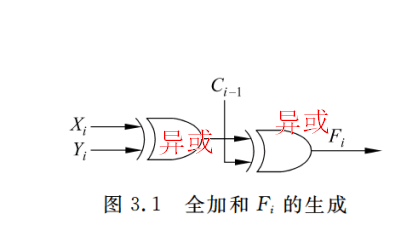
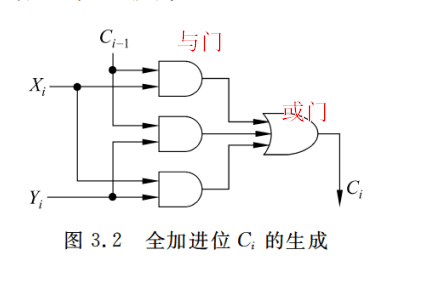
从3.2可以看出,进位输入到进位输出要经过2级门延迟,所以n位串行加法器从C0到Cn的延迟时间为2n级门延迟。
串行加法器的缺点:运行速度慢,因为进位按串行方式传递,高位进位依赖低位进位。
并行进位加法器
并行进位加法器的提出是因为串行进位加法器采用串行逐级传递进位,电路延迟与位数成正比关系。CLA加法器=进位生成部件+进位传递部件+CLA部件+求和部件

由上式可知,各进位之间无需等待,可以相互独立同时产生。
带标志加法器
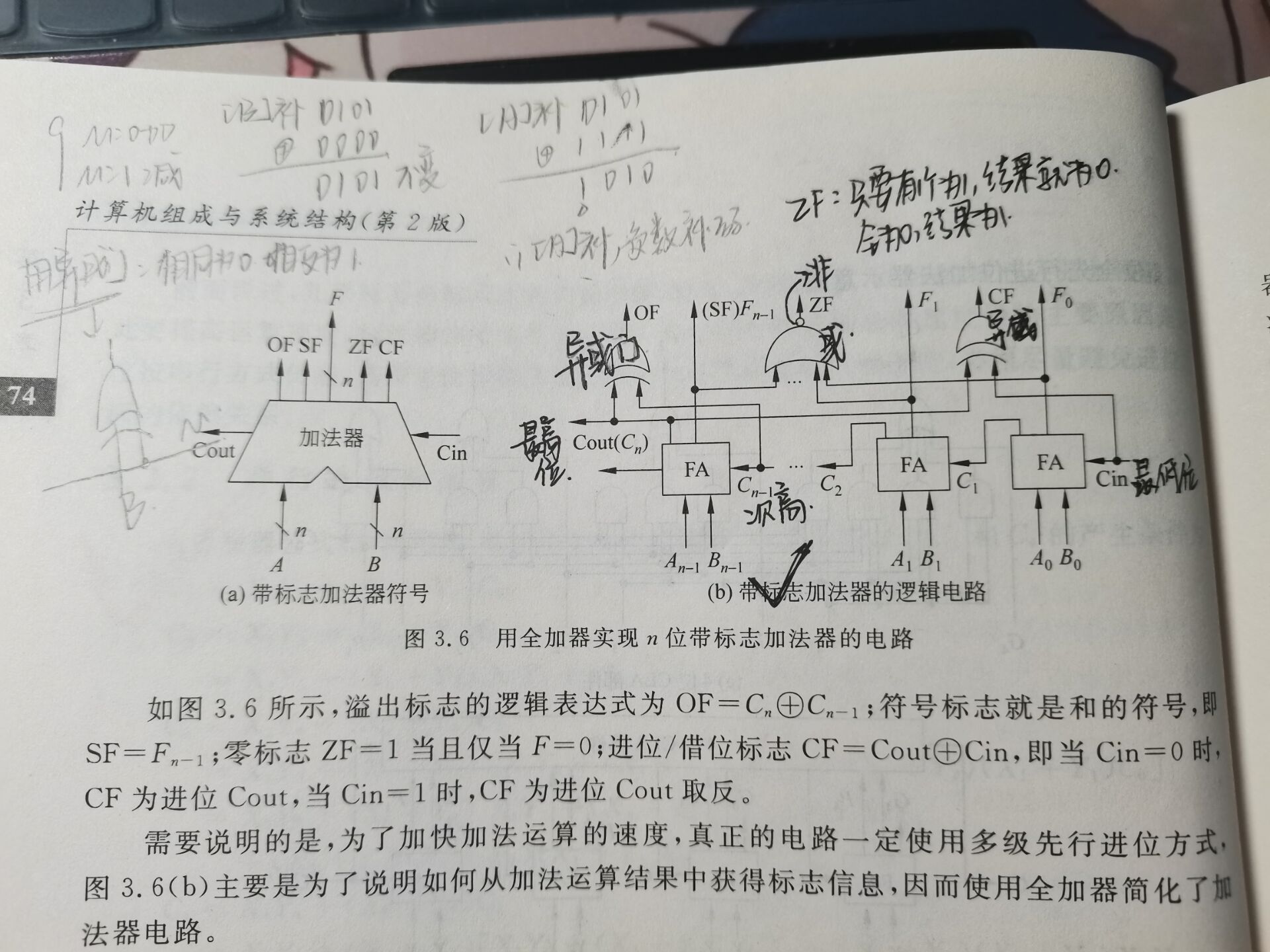
- 计算机中所有算术运算都基于加法器实现!
- 加法器不知道所运算的是带符号数还是无符号数。
- 加法器不判定对错,总是取低n位作为结果,并生成标志信息。
1 | OF溢出标志:是针对有符号数运算的情况 |
定点数运算及其运算部件
补码加减运算
1 | 补码的定义 假定补码有n位,则: |
1 | 根据补码定义,有如下公式: |
整数加法
做加法时,主要判断是否溢出
- 无符号加溢出条件:CF=1,CF=Cin⊕Cout
- 有符号加溢出条件:OF=1,OF=Cn⊕Cn-1
例如,n=8,计算107+46=?
(107)~10~=(0110 1011)~2~
(46)~10~=(0010 1110)~2~
相加= 1001 1001
无符号数:(1001 1001)~2~=+153,CF=0⊕0=0,不溢出
有符号数:(0 1001 1001)~2~=-103,OF=0⊕1=1,溢出
整数减法
做减法比较大小时
- 无符号:CF=0时,前者大于后者
- 有符号:OF=SF时,前者大于后者
例如,2-3
无符号数 2-3,
(2)~10~=0010
(-3)~补~=1101
相加=1111,CF=1⊕0=1,2<3
有符号数2-3,
(2)~10~=0010
(-3)~补~=1101
相加=1111,SF=1,OF=0⊕0=0,SF≠OF,2<3
浮点数运算及其运算部件
关键是 把小阶码转化为大阶码
例如: 0.123 × 10^5^ + 0. 560 ×10^2^
0.123 ×10^5^ + 0.560 ×10^2^= 0.123 ×10^5^+ 0.000560 ×105^5^ =(0.123 + 0.00056) ×10^5^= 0.12356 ×10^5^



